일단 트리구조는 그 자체만으로는 데이터값에 대한 어떠한 제약도 없기때문에,
어떤 특정한 값을 찾기위해서는 트리의 모든 데이터를 탐색해야하는 상황이 발생한다.
그러면 데이터 N개만큼의 탐색을 진행해야하기 때문에 시간복잡도면에 있어서 좋지 않다.
이런 문제를 해결하기위해 이진탐색트리가 나오게되었는데, 이진탐색트리는 데이터의 특성에 제약을 줌으로써 탐색속도를 O(logN)으로 줄여주는 특징이 있다.
이진트리와 이진탐색트리 비교
이진탐색트리는 기본적으로 왼쪽 자식노드와 오른쪽 자식노드를 가질 수 있다는 점에서 이진트리와 같은 구조라고 볼 수 있다.
그러나 일반적인 이진트리와의 차이점은 데이터값에 제약이 생긴다는것이다.
이진탐색트리에서는 루트노드를 기준으로 왼쪽서브트리는 루트노드보다 작은값들로만 이루어져있어야하고,
오른쪽 서브트리는 루트노드보다 큰 값들로만 이루어져있어야한다.
이것이 이진트리와 이진탐색트리의 차이점이다.
그리고 각각 왼쪽 서브트리와 오른쪽 서브트리 모두 이진탐색트리를 구성하고 있을때!! 이진탐색트리라고 한다.

이진탐색트리(BST)
아래 그림을 보면서 설명해보면
루트노드 5를 기준으로 왼쪽서브트리는 5보다 작은값, 오른쪽서브트리는 5보다 큰값이 들어가 있는것을 확인할 수 있다.
그리고 각각의 왼쪽 서브트리와 오른쪽 서브트리를 봤을때도 왼쪽 서브트리의 루트노드인 3을 기준으로 왼쪽은 3보다 작은값, 오른쪽은 3보다 큰 값이 있어야한다.
오른쪽 서브트리도 역시 서브트리의 루트노드인 7을 기준으로 왼쪽은 7보다 작은값, 오른쪽은 7보다 큰값으로 이루어져있어야한다.
이런식으로 계속해서 하위에 서브트리를 계속 타고 들어가더라도, 해당 이진탐색트리의 특징이 유지되어야한다!!
한 노드라도 이런 특성이 유지되지 않는다면 그 트리는 이진탐색트리라고 할 수 없다!

이진탐색트리(BST)의 특징
이진탐색트리의 최소값은 트리의 레벨에 관계없이 트리의 가장 왼쪽 끝에 위치한 노드가 된다는 것이다.
아래 그림상에서 봤을때, 가장 왼쪽에 위치한 1이 실제로 가장 작은값임을 확인할 수 있다.
(만약 1노드에 왼쪽자식이 존재하게된다면 그 노드에 있는 값이 가장 최솟값이 될것이다.)

반대로 최댓값도 트리의 레벨에 관계없이 트리의 가장 오른쪽 끝에 있는 노드가 된다.
그림상에서는 9가 가장 오른쪽 끝에 있는 노드로, 가장 큰값임을 확인할수있다.

그래서 이진탐색트리는 루트의 데이터값이 항상 왼쪽 서브트리보다는 크고, 오른쪽 서브트리보다는 작은 특징때문에
중위탐색(왼쪽 - 루트 - 오른쪽)으로 탐색을 진행할경우, 모든 데이터값을 정렬된 순서로 가져 올 수 있다는 특징이 있다.
중위탐색으로 탐색을 진행하면
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9 순으로 정렬된 순서로 방문하게 되는것을 확인할 수 있다.
이진탐색트리의 데이터 삽입
트리또한 데이터 삽입,삭제와 관련된 연산이 당연히 가능하다.
이진탐색트리의 데이터 삽입은 어떻게 진행될까?
기본적으로 이진탐색트리는 중복된 데이터는 삽입하지 않고, 데이터의 삽입이나 삭제가 진행되도 이진탐색트리의 기본특성이 유지되어야한다!! (어떤 서브트리를 보던간에 루트노드보다 왼쪽에 있는값은 루트보다 작고, 오른쪽에 있는값은 루트보다 커야함)

예를 들어, 이 그림과같은 트리에서 1이라는 데이터를 삽입한다고 해보자.
제일 먼저 루트노드인 8과 비교연산을 하게되고, 8보다 값이 작기 때문에 왼쪽 서브트리로 이동하게된다.
8의 왼쪽자식노드인 5를 만나서 다시 비교연산을 하게되고 역시 5보다 작기때문에 다시 왼쪽 서브트리인 2로 이동하게된다.
2와 비교연산을 했을때 2보다 작기때문에 역시 왼쪽 서브트리로 이동하게된다.
근데 이제 더이상 타고들어갈 왼쪽 서브트리가 없기때문에 2의 왼쪽 자식노드로 1이 추가되면서 삽입연산이 종료될것이다!
따라서 최종적으로 아래와 같은 트리모양이 나올것이다.

이진탐색트리의 데이터 삭제
삭제는 삽입보다는 몇가지 더 생각해야할것이 있다.
삭제를 할때는 트리의 리프(leaf)노드만 삭제되는것이 아니라 중간에 위치한 노드가 삭제될수도 있기 때문이다.
따라서 삭제할때는 3가지 경우에 대해서 모두 생각해봐야한다.
1) 삭제 할 데이터가 leaf 노드에 있는 경우
2) 한개의 자식노드를 가진 경우
3) 두개의 자식노드를 가진 경우
1) 삭제 할 데이터가 -> leaf 노드에 있는 경우
삭제할 데이터가 leaf노드에 있는 경우를 먼저 볼것이다.
위의 그림을 봤을때 2와 8을 삭제하는 경우가 될것이다.
이때는 null을 부모노드에게 리턴시켜서 자신에게 가리키던 자식포인트를 null로 가리키게 해준다.
그래서 2를 삭제하면 부모노드였던 1은 오른쪽 자식노드로 null값을 가지게되고, 8을 삭제하면 부모노드였던 9는 왼쪽 자식노드로 null값을 가지게되면서 데이터가 삭제된다.

2) 삭제 할 데이터가 -> 한개의 자식노드를 가진 경우
이제는 한개의 자식노드를 갖는 데이터를 삭제하는 경우다.
하나있는 자식노드를 부모노드로 보내주면 된다.
그림에서 1노드를 삭제해줄건데, 1의 자식노드인 2를 3의 자식노드로 보내주면 된다!
이렇게하면 이진탐색트리의 속성을 유지하면서 데이터를 삭제할 수 있게 된다.

2) 삭제 할 데이터가 -> 두개의 자식노드를 가진 경우
마지막으로 두개의 자식노드를 가지고 있는 데이터를 삭제할 경우를 살펴볼것이다.
이때는 또 두가지 방법으로 나눠볼 수 있다.
1. 노드의 왼쪽 서브트리의 최대값이 삭제할 노드의 위치에 오도록 보내주기!
2. 노드의 오른쪽 서브트리의 최소값을 삭제할 노드의 위치에 오도록 보내주기!
둘중 어느방법을 사용해도 상관없다
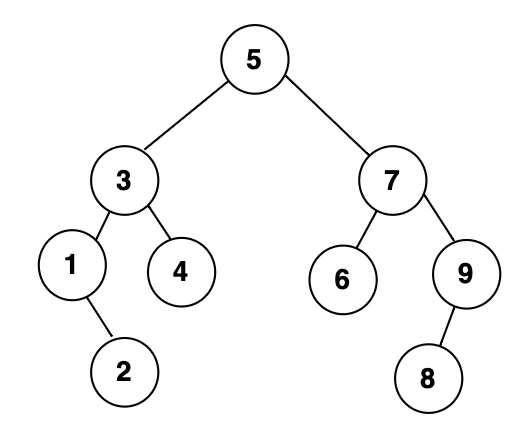
두개의 자식노드를 가진 7노드를 삭제하는 경우를 살펴볼건데,
먼저 첫번째 방법부터 살펴보겠다.

노드7을 삭제해야되기 때문에, 7의 왼쪽 서브트리에서 최대값은 6이 될것이다.
그렇기 때문에 7노드 자리에 6이 대신 들어오게 될것이다
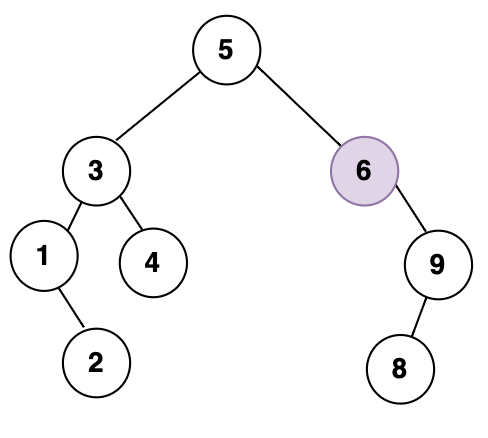
그러면 이런 트리모양이 나오게 될것이고, 노드 7이 잘 삭제가 된 것을 볼 수 있다
이진탐색트리의 기본특성도 잘 만족하는 것을 확인할 수 있다.
이제 두번째 방법을 살펴보겠다.

노드7을 삭제해야되기 때문에, 7의 오른쪽 서브트리에서 최소값은 8이 될것이다.
그렇기 때문에 7노드 자리에 8이 대신 들어오게 될것이다

그럼 위와같은 트리 모양이 그려지게 될것이다.
근데 이진탐색트리는 중복되는 데이터가 없어야되기 때문에, 중복되는 데이터인 리프노드에 있는 8노드를 삭제해줘야한다.
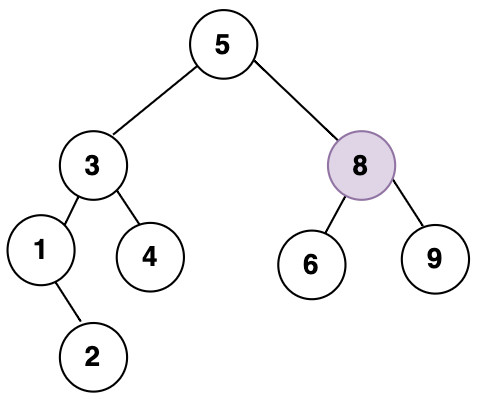
따라서 최종적으로 이렇게 두개의 자식노드를 가진 데이터의 삭제가 이루어지는 것을 볼수있다.
'개발 노트 > 자료구조' 카테고리의 다른 글
| [자료구조] 그래프(Graph) (0) | 2024.08.03 |
|---|---|
| [자료구조] 이진힙[힙](heap) (0) | 2024.07.26 |
| [트리순회] 후위탐색(postorder) (0) | 2024.07.26 |
| [트리순회] 중위탐색(inorder) (0) | 2024.07.26 |
| [트리순회] 전위탐색(preorder) (0) | 2024.07.26 |



