그래프란?
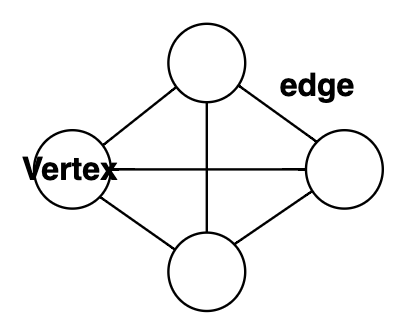
그래프는 vertex와 edge로 구성된 대표적인 비선형 자료구조이다.
vertex는 트리에서 노드와 비슷한 개념이고, edge는 vertex간의 연결관계를 나타내는 선이다.
두 vertex가 edge로 연결되어있을때, 두 vertex는 "인접해있다" 고 한다.
트리도 그래프의 일종이지만, 그래프는 트리보다 훨씬 더 넓은 범위를 포함한다.
그래프의 종류
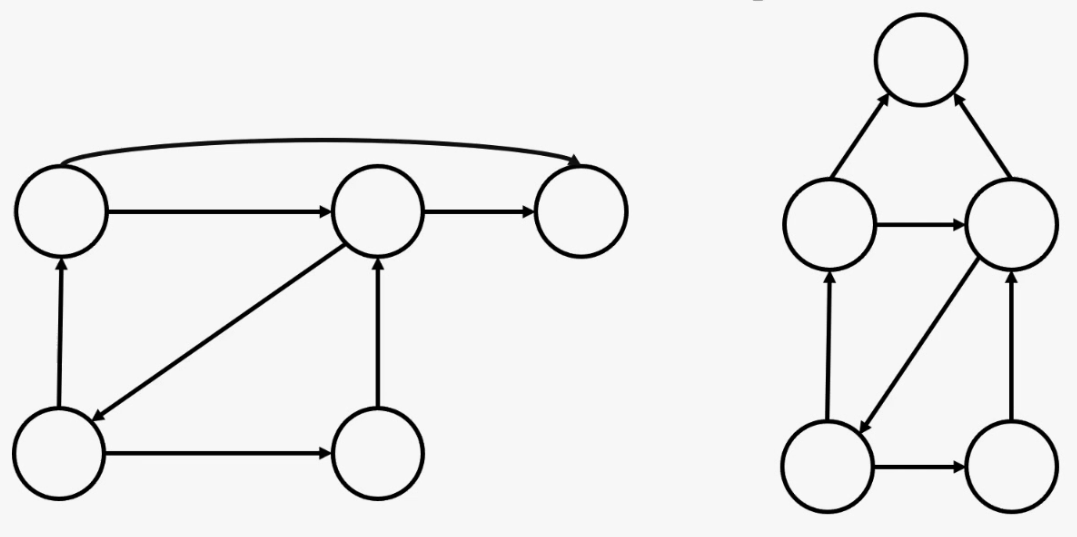
- 방향 그래프 (directed graph)
화살표를 이용해서 방향을 표시할 수 있는 그래프를 방향그래프라고 한다.
방향 그래프는 무조건 방향의 순서대로만 노드를 이동시킬 수 있다.
방향이 없는 그래프는 무방향 그래프(undirected graph)라고 한다.
- 가중치 그래프 (weighted graph)
가중치 그래프는 아래그림처럼 edge에 가중치가 부여된 그래프다.
이 가중치는 양수일수도 있고, 음수일수도 있다.

위의 그래프에서 보면 A에서 B로 이동할 수 있는 경로는
[A-B] , [A-C-B] 이렇게 두가지 경우가 있을것이다.
만약 가중치가 없다면 [A-B]가 더 빠른 방법이겠지만, 가중치가 있기때문에 해당 경로는 7이라는 비용을 소모하게된다.
그치만 [A-C-B] 이 경로로 가면 3이라는 비용밖에 소모하지 않기때문에, 이렇게 C를 거쳐가는 것이 더 효율적인 방법일것이다.
이렇게 가중치가 있는 그래프에서 다익스트라 알고리즘을 사용해서, vertex에서부터 다른 vertext까지의 최단경로를 찾을 수 있다.
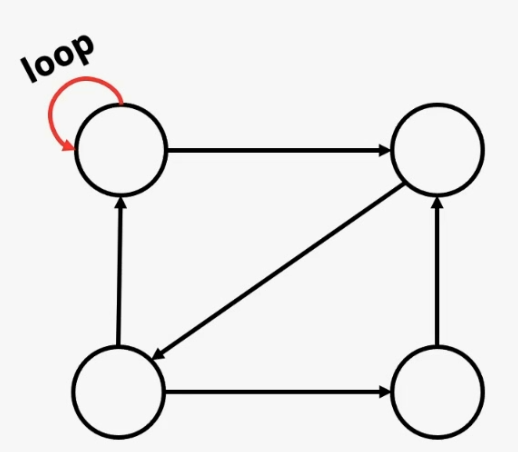
그리고 그래프의 vertex는 자기자신을 가리키는 edge를 가질수도 있다.
그때 이 edge를 루프(loop)라고 한다.
loop는 자기자신으로 다시 돌아오는 것을 뜻한다.
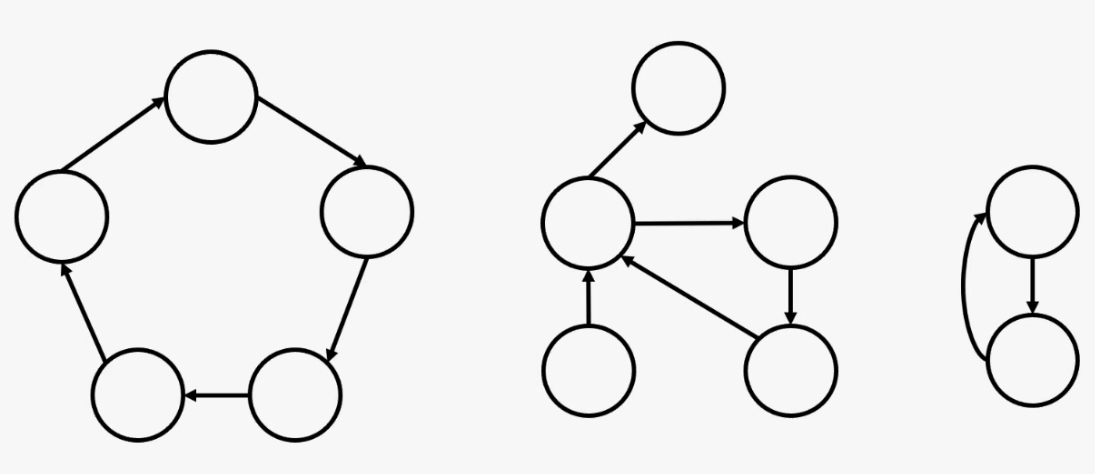
- 순환 그래프 (cyclic graph)
순환그래프는 한 vertex에서 경로를 지나서 다시 그 vertex로 돌아오는 그래프를 말한다.
즉, 사이클이 있는 그래프를 순환그래프라고한다.
트리와 그래프의 가장 큰 차이점을 꼽자면 사이클의 유무인것같다.
트리는 사이클이 없고, 방향이 있는 방향 비순환 그래프(directed uncyclic graph)의 한 종류라고 볼 수 있다.
그래프 구현
그래프를 구현하는 방법은 크게 인접행렬방식, 인접 리스트방식 2가지가 있다.
1) 인접 행렬 방식
인접행렬은 그래프를 2차원 배열로 표현할 수 있는 방식이다.
연결된 vertex의 위치에는 1, 연결되지 않은경우에는 0이나 음수를 넣어서 2차원배열로 표시하는 방법이다.

인접행렬방식은 직접적으로 vertex간의 연결정보를 파악하기 쉽다는 장점이 있지만,
노드(vertex)개수가 n개라면 위에 표에서보다시피 n제곱에 해당하는 메모리 공간을 사용해야한다는 단점이 있다.
또한 edge를 추가하거나 삭제하는 연산은 간단하지만, 새로운 노드(vertex)를 추가할경우에는 연산의 복잡도가 올라가는 단점 또한 존재한다.
2) 인접 리스트 방식
인접리스트방식은 vertex의 개수만큼만 list를 생성하는 방식이다.
따라서 해당 노드(vertex)를 기준으로 연결된 vertex만 리스트에 저정하게된다.
A는 B,D와 연결이 되어있으므로 B,D만 리스트에 저장하게되고,
B는 A,C와 연결이 되어있으므로 A,C만 리스트에 저장하게 된다. 나머지 vertex도 똑같이 적용이 될것이다.
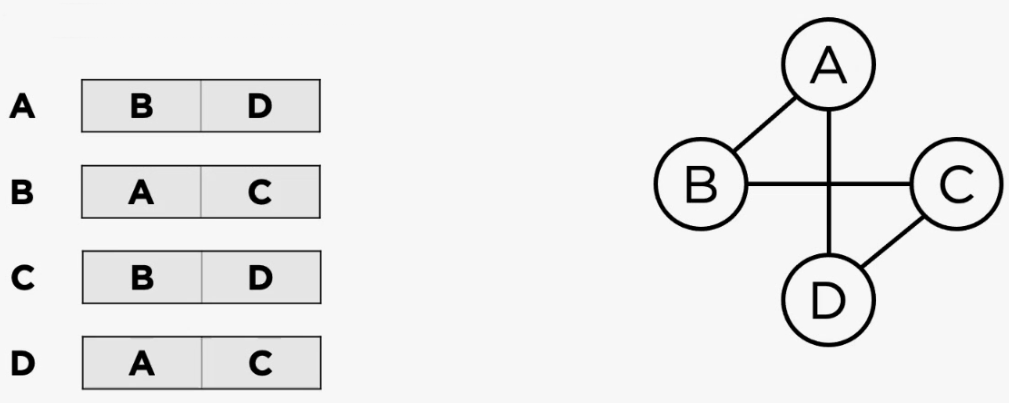
인접리스트 방식은 인접행렬보다 메모리 공간을 효율적으로 사용할 수 있다는 장점이 있다.
또한 새로운 노드(vertex)를 추가하거나 삭제할때도 인접행렬보다 훨씬 수월하다.
하지만 리스트만보고 vertex의 연결관계를 파악하기에는 인접행렬보다는 힘들다는 단점이 있다.
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] 이진탐색트리(BST - Binary Search Tree) (0) | 2024.07.26 |
|---|---|
| [자료구조] 이진힙[힙](heap) (0) | 2024.07.26 |
| [트리순회] 후위탐색(postorder) (0) | 2024.07.26 |
| [트리순회] 중위탐색(inorder) (0) | 2024.07.26 |
| [트리순회] 전위탐색(preorder) (0) | 2024.07.26 |



