배열, 리스트, 스택과 큐, 해시테이블과 같은 자료구조는 데이터의 이전 데이터나 다음 데이터의 순서가 존재하는 선형 자료구조에 해당한다.
이러한 구조는 특정 데이터를 검색할때 순서대로 데이터를 찾아야하는 문제점과,
데이터를 저장하기위해 일정한 공간을 미리 할당해야하는 등의 제한적인 구조를 가지고있어 복잡한 문제를 해결하는데 어려움이 있다.
대표적인 문제로는 계층적 문제와 순환 종속성 문제가 있다.
계층적 문제란 계층적 속성을 갖는 자료는 선형구조로 표현하기가 어렵다는 것을 뜻한다
순환 종속성 문제란 두개 이상의 요소가 서로 순환적으로 의존하여 발생하는 문제를 뜻하는데, 이또한 선형구조로 표현하기에는 어려움이 있다.
따라서 이러한 단점들을 개선하기위해 비선형 자료구조가 나오게되었다
비선형 자료구조는 크게 트리와 그래프로 나눌수있다.
이런 비선형 자료구조를 사용하면, 데이터를 더욱 효율적으로 검색하고 저장할 수 있고 데이터의 계층적인 관계를 표현하기에 용이하다.
이번에는 비선형 자료구조중 하나인 트리를 공부해볼것이다
트리(Tree)란?
한 노드가 여러 노드를 가리킬 수 있는 비선형적 자료구조이다.
트리는 순서보다는 데이터 구조의 계층적인 상하관계를 표현할 때 주로 사용한다. 그래프라는 자료구조의 일종이라고 볼 수 있다.
트리는 이런 구조를 갖고있어 데이터 삽입,삭제,검색 등이 효율적으로 이루어지며, 데이터의 계층적인 관계를 표시하기에 매우 용이하다.
그치만 불균형한 트리일경우(노드의 서브트리가 한쪽으로 치우친경우) 검색속도가 느려질수있고, 트리의 크기가 커질경우 메모리 공간을 많이 차지한다는 단점도 존재한다.
트리구조에 가장 대표적인 실생활 예제로는 컴퓨터의 디렉토리 구조를 예로 들수있다. (상위폴더 -> 아래폴더 -> 그 아래폴더....)
트리구조 도식화
컴퓨터의 디렉토리 구조에서 보면 가장 상위폴더가 있고, 그 아래 하위폴더, 또 그아래 하위폴더가 있는 구조일것이다.
이런식으로 데이터간에 상하위 관계가 존재하는 데이터구조를 표현하고자할때 트리를 사용할 수 있다
아래 그림처럼 표현할 수 있다

트리구조 - 노드(Node), 루트(Root), 엣지(Edge)
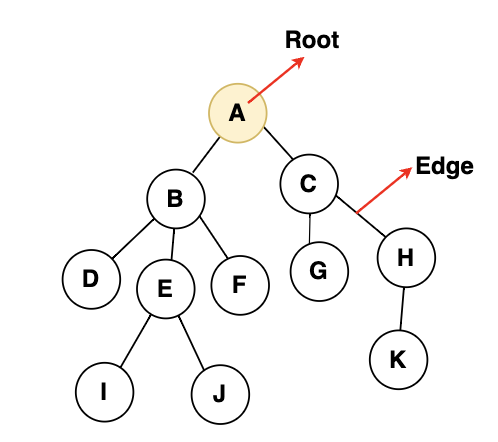
A데이터가 가장 상위에 있고, 하위에 B와 C의 데이터를 가지고 있죠. 그리고 B는 하위로 D,E,F의 데이터를, C는 G,H의 데이터를 가리키고 있다.
이런식으로 트리를 구성하는 각 데이터 원소 하나하나들을 노드(Node)라고 한다.
트리에서 부모가 없는 최상의 노드를 루트노드(Root Node)라고 한다. 루트는 트리의 시작점이 되고, 트리는 최대 1개의 루트만 가질 수 있다.
그리고 이 노드를 연결하는 노드들간의 선을 엣지(edge)라고한다.
그래서 트리는 루트(Root)로 부터 시작해서 엣지(edge)로 연결된 노드(node)들로 구성되어있다고 말할수있다.
트리구조 - 부모노드, 자식노드, 형제노드, 리프(leaf)노드
트리의 계층적 속성에서 상위에 존재하는 노드를 부모노드
부모노드의 하위에 위치한 노드를 자식노드
같은 부모를 갖는 노드를 형제노드 라고한다.
그림에서 A는 부모노드가 될수있고, B,C는 A노드의 자식노드가 될것이다.
B,C는 같은 부모를 두었기때문에 B,C는 서로 형제노드라고 볼수있다
근데 B,C는 A를 기준으로하면 자식노드이지만, 각자 하위에 노드를 가지고있기때문에 부모노드도 될 수 있다.
즉, D,E,F 노드에 있어서 B는 부모노드가 될수있고, C도 마찬가지로 G,H에 대해서는 부모노드가 될수있다.
따라서 부모노드와 자식노드는 상대적인 개념이라고 생각하면 될것이다
그리고 각 노드의 자식수는 차수(degree)로 표현할수있다
B노드는 자식을 3을 가진 degree3의 노드가 된다.
마지막으로 자식이 없는 노드는 낙엽을 뜻하는 리프(leaf)노드라고 부른다. 그림에서는 D,I,J,F,G,K가 리프노드일것이다.

트리의 경로(path)
노드에서 다른 노드에 이르는 사이의 노드순서를 경로(path)라고 한다.
그래서 A노드부터 K노드까지의 경로는 [A - C - H - K] 노드가 될것이고,
이때 경로는 중복 노드를 포함하지 않는다!!
즉, A부터 F까지의 경로는 [A - B - F]로 표현하지,
[A - B - E - B - F] 이런식으로 노드를 중복해서 표현하지 않는다는것이다

추가로, 트리에는 사이클(cycle)이 존재할 수 없다!
사이클이란 아래그림처럼 시작노드에서 출발해 다른 노드를 거쳐 다시 시작노드로 돌아올 수 있는것을 뜻한다.
하지만 트리는 부모 -> 자식 노드로만 이어져 있기 때문에 처음 정점이 끝 정점이 되는 일은 없기 때문에 사이클을 이루지 않는구조이다.

트리의 깊이(Depth)
해당노드에서 Root까지의 거리를 깊이(Depth)라고한다
노드 B,C는 루트로부터 깊이가 1인 위치에 있고,
노드 D,E,F,G,H는 루트로부터 깊이가 2인 위치에 존재한다.
마지막으로 I,J,K는 깊이가 3이므로 해당 트리에서 가장 깊은 깊이를 가지게된다!
이렇게 가장 큰 깊이는 트리의 높이라고 표현한다!!
트리의 레벨(Level)
그리고 같은 깊이(depth)를 가진 노드의 집합을 그 트리의 레벨이라고 한다
우선 루트노드는 level 0에 있게되고,
B,C / D,E,F,G,H / I,J,K 가 각각 같은 집합의 레벨로 묶일것이다

트리의 서브트리(SubTree)
트리의 하위노드는 서브트리를 구성하는 재귀적인 특징을 갖는다.
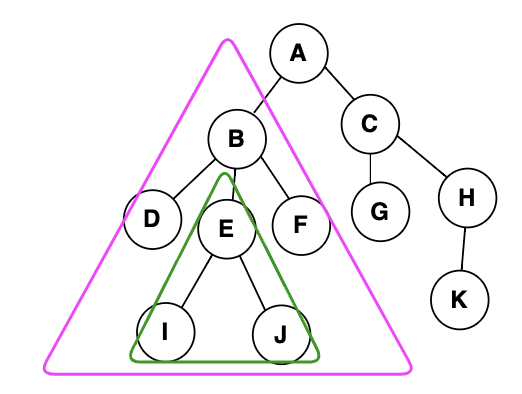
A를 루트로 하는 전체 데이터는 당연히 트리구성을 하고있을것이다.
그리고 A의 자식인 B를 루트로하는 하나의 서브트리로 볼 수 있다.
그리고 B의 자식인 E도 하나의 서브트리를 구성할 수 있다.
트리는 재귀적인 구조를 가지고 있는것이 굉장히 중요한 특징중 하나다!!
트리의 편향트리(경사트리)(skew tree)
앞에서 여태껏 본 모양은 당연히 모두 트리모양이라고 생각할것이다
그치만 아래 그림처럼 하위의 노드를 하나씩만 가지는 트리도 트리라고 볼 수 있다
편향트리(경사트리)는 모든 노드가 하나의 자식만을 가지는 경우를 말한다.
왼쪽 방향으로 자식을 하나씩만 가질 때 left skew tree(왼쪽 편향트리), 오른쪽 방향으로 하나씩만 가질 때 right skew tree(오른쪽 편향트리) 라고 한다.

트리 구분
이렇게 트리의 전체적인 특징에 대해서 살펴봤는데, 아래그림을 보면서 트리가 맞는지 아닌지 살펴보겠다

그림1은 트리라고 할수없다. D에서 시작해 B,C,E를 거치고 다시 D로 오기때문에 사이클이 존재하기 때문이다.

그림2도 트리라고 할수없다. 사이클은 없지만, 1에서 시작해 4로 가는 경로가 유일하지 않기때문이다.
1에서 4로 가는경로는 [1 - 2 - 4]로도 갈수있고 [1 - 3 - 4] 를 통해서도 갈 수 있기때문에 트리가 아니다.

그림3도 트리가 아니다. 모든 노드들이 연결되어있어야하는데 B,D는 연결되어있는 상태가 아니기때문에 트리가 아니다.
만약 B,D만 잘 연결되어있는 상태라면 트리구조가 맞다
이렇게 트리에 대해서 학습해봤다
이런 트리는 특성에 따라서 여러 종류로 세분화할 수 있다
이진트리, AVL트리, B-트리, B+ 트리 등 여러가지로 세분화할 수 있다.
해당 트리들도 학습해봐야겠다
'Computer Science > 자료구조' 카테고리의 다른 글
| [트리순회] 전위탐색(preorder) (0) | 2024.07.26 |
|---|---|
| [자료구조] 이진트리 (Binary Tree) (0) | 2024.07.26 |
| 정렬 알고리즘[Quick Sort] (0) | 2024.07.22 |
| 정렬 알고리즘[Merge Sort] (0) | 2024.07.22 |
| 알고리즘[시간복잡도] (0) | 2024.07.22 |



